L'ombre et le bâton

Pour mesurer le rayon de la Terre, il vous faut un bâton, un bâton droit, que les astronomes appellent un gnomon.

Plantez le perpendiculairement à une surface plane et horizontale, et placez le tout au Soleil. Pour vous assurer de l'horizontalité, utilisez un niveau à bulle si nécessaire. S'il fait beau, vous ne manquerez pas de remarquer l'ombre du bâton. Rien d'étonnant me direz vous ? C'est vrai, mais c'est avec deux dispositifs comme celui-ci que je vous demande de déterminer le rayon de la Terre ! Un peu de réflexion...

1. Le triangle rectangle, je maîtriserai

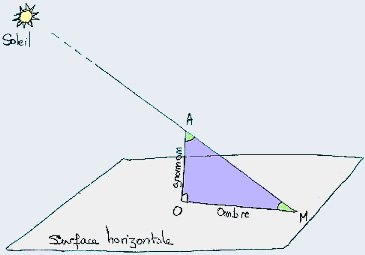
La figure représente votre gnomon. Le triangle AOM est rectangle. Nous pouvons facilement déterminer les deux angles (OAM) et (OMA) en fonction de quelques distances : la longueur OA du gnomon et la longueur OM de l'ombre.

Pour mesurer le rayon de la Terre, seul l'angle (OAM) nous intéresse. Pour faciliter les mesures je vous conseille de faire l'expérience lorsque le Soleil se trouve au plus haut dans le ciel, c'est-à-dire lorsqu'il est exactement au dessus du sud. En France, cela se produit aux environs de 13h pendant l'heure légale d'hiver et de 14h pendant l'heure légale d'été.

Une boussole se révèlera précieuse pour tracer l'axe nord-sud passant par le pied du gnomon. À l'instant qui nous intéresse, son ombre et cet axe se confondent.

2. Les rayons solaires, je vénérerai

Étant donné la très grande distance de la Terre au Soleil et la dimension toute relative de la Terre, nous pouvons considérer que les rayons solaires qui parviennent à la surface de la Terre sont tous parallèles.

3. Mes données, je partagerai

Dégainez votre téléphone portable, ouvrez votre logiciel de messagerie favori, sortez votre plus belle plume, que sais-je ? Car il vous faut maintenant trouver de l'aide. Partez à la recherche d'une personne, pourquoi pas d'une classe, qui se trouve sur la même longitude que vous mais à une latitude sensiblement différente. À vos atlas ! Plus la différence de latitude sera grande, plus votre résultat sera précis ; restez cependant raisonnables, il n'est pas nécessaire de déranger nos voisins étrangers. Vous devrez ensuite connaître la distance qui vous sépare à vol d'oiseau. Une carte d'état major fera très bien l'affaire.

Expérience virtuelle

Peut-être ne trouverez-vous personne d'aussi curieux que vous ? Peut-être le Soleil ne sera-t-il pas au rendez-vous ? Peut-être souhaiterez-vous vérifier vos mesures de fous ?

Je vous propose ce petit programme. Dites-lui la longueur de votre gnomon, la date et le lieu de l'observation, il vous les échangera contre quelques informations précieuses.

Solution

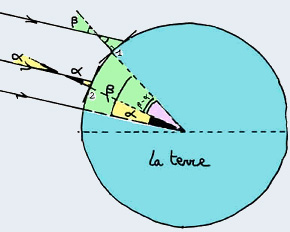
Vous qui êtes en position 1, déterminez l'angle b grâce à l'ombre de votre gnomon (sa taille est exagérée sur le dessin mais les angles ne changent pas).

Votre ami(e) en position 2 détermine l'angle a grâce à l'ombre de son gnomon.

Vous échangez vos mesures et, en reportant ces angles, vous déterminez ensemble la différence de latitude entre vos deux sites d'observation : b - a.

En utilisant une carte, vous déterminez la distance qui vous sépare. Sur le dessin, il sagit de l'arc de cercle sous tendu par l'angle b - a. En appliquant la relation simple entre la longueur d'un arc de cercle, l'angle sous tendu et le rayon du cercle, vous obtenez la longueur de l'arc de cercle (1,2).

Puis, par la relation longueur de l'arc (1,2) = Rayon Terre * (b-a), vous déterminez le rayon de la Terre :

Rayon de la Terre = longueur de l'arc (1,2) / (b - a )

Rayon théorique

Le rayon théorique moyen de la Terre est de 6 378 km. Vous n'obtiendrez bien sûr pas une telle précision, mais vous obtiendrez tout de même un résultat assez proche. Cette valeur est une valeur moyenne. La terre n'est pas parfaitement sphérique mais plus aplatie aux pôles qu'à l'équateur. L'effet provient de la rotation de la Terre sur elle-même qui tend en quelques sortes à la gonfler à l'équateur.

Un peu d'histoire...

En -350 av. J.-C., le scientifique Eratostène a mesuré le rayon de la Terre par cette méthode. À midi, par une belle journée, il avait remarqué à Assouan (anciennement Syène) que le fond des puits étaient éclairés par le Soleil. Ce n'était pas le cas, au même moment, pour l'un de ses collègues à Alexandrie, qui mesura l'angle formée par l'ombre d'un gnomon. En connaissant la distance entre les deux villes (avec la mesure de l'époque), Eratostène donna une première estimation du rayon de la Terre. La distance entre les deux cités était estimée à cette époque à 5000 stades, un stade faisant 157 m.

Retour à la liste des expériences interactives