Mesurer la distance qui nous sépare des étoiles :
la méthode de la parallaxe.

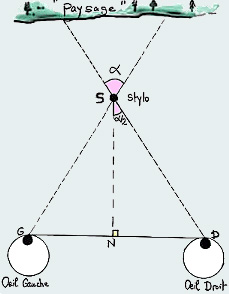
Question : Tendez un stylo à bout de bras et fermez alternativement un oeil, puis l'autre. Que constatez-vous ?

Réponse : Le stylo semble se déplacer par rapport au paysage. On dit qu'il a un déplacement angulaire apparent.

Question : Écartez plus ou moins le stylo de vous et recommencez l'opération. Que constatez-vous ?

Réponse : plus le stylo est proche de vos yeux, plus son déplacement angulaire apparent semble important.

Un peu de Mathématiques (niveau 3e)

Dans le triangle rectangle (SND), nous allons déterminer la relation entre la distance NS qui nous sépare de l'objet, la demi-distance ND entre nos yeux, et l'angle alpha : tan(alpha/2) = ND / NS, soit NS = ND / tan(alpha/2).

Application à l'astronomie

Nos yeux sont trop rapprochés pour déterminer les distances importantes. La parallaxe devient trop petite pour être mesurée aisément. À moins d'être un géant avec deux yeux très éloignés l'un de l'autre, il est impossible de voir la distance des étoiles.

Pour déterminer la distance des étoiles proches, les astronomes ont pourtant trouvé une astuce.

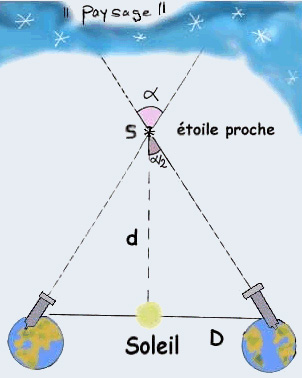
Ils pointent l'étoile proche qui les intéresse avec l'oeil d'un télescope et ils enregistrent une image.

Six mois plus tard, lorsque la Terre se trouve de l'autre coté du Soleil, ils refont la même opération.

Tous se passe comme si l'observation était faite par un géant avec des yeux distants de deux fois la distance Terre-Soleil, le paysage étant constitué par les étoiles très lointaines. On a donc d = D / tan(alpha/2) si l'étoile est située perpendiculairement au Soleil par rapport au plan du système solaire.

L'angle alpha/2 s'appelle la parallaxe et se note p. Cet angle est toujours très petit vu que la distance qui nous sépare des étoiles est considérable, et s'il est exprimé en radian (2pi radian = 360°), il est presque égal à sa tangente tan(p).

On simplifie donc fréquemment l'expression précédente par la relation d = D / p, où

– D est distance Terre-Soleil ;

– d est la distance Soleil-étoile ;

– p est la parallaxe (en radians).

Dans le cas général, en utilisant des unités propres à l'astronomie, l'expression devient d = 1 / p, où

– D = 1 équivaut à 1 unité astronomique, la distance Terre-Soleil

– d est la distance Soleil-étoile, en parsecs (1 parsecs =  3.086.10e13 km)

– p est la parallaxe, en secondes d'arc (1 seconde d'arc = 1 / 3600°)

Mesurez la distance des étoiles de la grande ourse

Les sept étoiles principales de la constellation de la grande ourse sont très populaires. Elles semblent former une grande casserole.

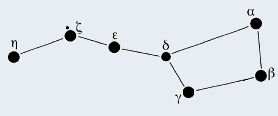
Lesquelles sont proches ? Lesquelles sont plus lointaines ? À quelles distances se situent-elles de nous ?

Le satellite Hipparcos a mesuré la parallaxe de plus de 120 000 étoiles proches avec une précision extraordinaire ! Le tableau ci-dessous donne les valeurs pour les sept étoiles principales de la grande ourse.

étoile	parallaxe (mas)	Incertitude (mas)
a (Dubhe)	26.38	0.53
b (Merak)	41.07	0.60
g (Phecda)	38.99	0.68
d (Megrez)	40.05	0.60
e (Alioth)	40.30	0.62
z (Mizar)	41.73	0.61
h  (Alkaid)	32.39	0.47

La parallaxe (mas) est la parallaxe en millisecondes d'arc, soit un 1/1000e de secondes d'arc. 1 seconde d'arc vaut 1/3600e de degré.

L'incertitude (mas) est l'incertitude sur la valeur de la parallaxe, en millisecondes d'arc.

Retour à la liste des expériences interactives